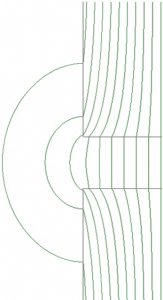
At the WoW conference during the Wireless Power Week, we presented two papers on the power handling capability and feasibility space of multilayer self-resonant structures (MSRS) for practical wireless power transfer (WPT) applications. A MSRS comprises many thin foil conductors with capacitive ballasting and equal current sharing among the layers and has demonstrated quality factor multiple times higher than similar size conventional WPT coils found in the literature.

First, we explore the power handling capability of the structure considering various large signal effects. These effects include nonlinear magnetic core loss, temperature rise and temperature dependence of losses. The analysis shows that the MSRS has a power capability at least 3 times higher than conventional WPT coils of similar size and thermal performance. A WPT system comprising two MSRS with 6.6 cm diameter and 3.5 mm thickness was able to transfer as much as 172 W over a distance of 3.3 cm (range/diameter = 0.5) when the measured surface temperature was 68 °C. The power capability is higher for shorter power transfer distance; the analysis shows that as high as 10 kW can be transferred over a 5 mm distance. Link to full paper

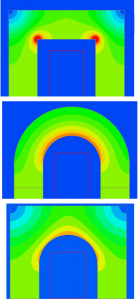
Second, we explore the minimum feasible resonant frequency and the maximum power level without dielectric breakdown that can be achieved using the MSRS given a size constraint.  This analysis is applied to two case studies; one for consumer electronics and one for electric vehicles. The example MSRS for electric vehicles has a diameter of 20 cm and height of 5 cm. If a 100 kHz resonant frequency is selected, the MSRS can achieve an output power of 10 kW at a range of 20 cm with an input voltage of 500 V.  Link to full paper

Improvements in performance of resonant coils are important for the range and efficiency of wireless power transfer (WPT); however, these improvements are difficult to measure using the conventional figure-of-merit (FoM), which is the product of quality factor and coupling factor.

In this paper, we proposed a new FoM that is an indication of the performance of a WPT coil technology independent of a specific implementation, and can be calculated using commonly reported parameters: coil diameter, transmission range, and coil-to-coil efficiency.

The new FoM is the ratio of the loss fraction of a reference system and and the system-under-test. The reference system models two-loops of solid wire that are scaled to the same overall size as the system-under-test.  We computed the FoM for a few WPT systems in the literature, and found the highest FoM to be 3.4, achieved using a self-resonant structure.

LINK TO PAPER

Of the three main component types needed in power converters—switches, capacitors and inductors—the most difficult to integrate on a semiconductor chip or in a planar package is the inductors. This difficulty arises partly from process compatibility challenges with magnetic materials, and is exacerbated by the fact that, because most types of electronics don’t need inductors, there has been relatively little development effort. But a more fundamental challenge is the way magnetics performance scales with size.

Capacitors and semiconductor devices can be made from thousands of small cells connected in parallel, but that approach would severely undercut the performance of magnetic components.

In this work, we examine the scaling relationships for magnetics to demonstrate the inherent difficulty of small size and low profile magnetics. Cases considered include those with winding designs limited by skin and proximity effect and those constrained by efficiency and thermal dissipation. Small-scale magnetic components are typically limited by efficiency rather than heat dissipation. With efficiency constrained, and considering high frequency winding loss effects, it is shown that power density typically scales as the linear dimension scaling factor to the fifth power.

For the full analysis, see the attached paper, Sullivan, C.R., Reese, B.A., Stein, A.L. and Kyaw, P.A.,. “On size and magnetics: Why small efficient power inductors are rare.” IEEE International Symposium on 3D Power Electronics Integration and Manufacturing (3D-PEIM), 2016.

There’s a lot we know about magnetic core loss, and at lot we don’t know.  The situation is summarized in presentation slides from my presentation at the PSMA/IEEE Magnetics Workshop.  The slides have the references added at the end with reference numbers sprinkled through.

People were intrigued by the three simple flux crowding simulations shown here.  These aren’t intended to be highly accurate–they are based on constant permeability, and as pointed out by Bruce Carsten, the real behavior is nonlinear.  But the results are still interesting and somewhat surprising.  Based on loss proportional the flux density raised to the 2.5 power, the second picture–the circular hoop–doesn’t reduce loss as you might expect.  Rather, it raises loss by about 3%, compared to the simple square corners at the top.  But the bottom design does reduce loss, by about 8%, compared to the simple square corners.

Our new paper accepted for publication in IEEE Transactions on Power Electronics (pdf) explores the potential for new types of passive components and shows that there are exciting opportunities.

• Analysis of volumetric energy densities of various storage mechanisms shows that mechanical storage may offer order-of-magnitude improvement over conventional electromagnetic passive components.
• Considering only the limitations imposed by material properties and not by available fabrication methods, both piezoelectric and LC resonators have fundamental performance limits that are much higher than the capabilities of commercial passive components in use today.
• A prototype 1 cm³ integrated LC resonator optimized for low loss is capable of handling 7.42 kW with only 0.06% loss attributable to the resonator when used in a resonant switched-capacitor circuit.

The high-Q achievable by self-resonant structures increases the range and efficiency of wireless power transfer (WPT). However, to date implementations of this structure have been thick, which limits their practical implementations. In the attached paper, we explore the design of thin self-resonant structures.

We describe:
1) a computationally efficient 2-D optimization algorithm is proposed to design thin
resonant structures and illustrate the trade-offs in the design, and
2)a new magnetic core shape is proposed which shapes the magnetic field lines to be parallel to the conductive layers and reduces current crowding.

These advances results in a prototype 3.5 mm thick self-resonant structure, which has a measured quality factor of 560 despite having a diameter of only 6.6 cm; this provides a 3.03× improvement over the state-of-the-art WPT coils in the literature.

See a full description of the thin structure in the attached paper

Matching networks have useful applications in transforming voltages and impedances in resonant inverters and dc-dc converters. Stacking multiple stages of matching networks can, in some cases, increase the efficiency because each stage is responsible for smaller transformation, but it also reduces the available inductor volume for each stage which can increase the loss.

At COMPEL 2017, we presented a paper (link for pdf) on optimization of matching networks with volume constraints to determine the optimum number of stages and other design choices for various transformation ratios, volumes and impedances. Adding the volume constraint to the typical matching network design process helps provide a better perspective on the number of stages that should be used. Simple design rules for designing matching networks, with a constraint on the available volume, are presented for voltage transformation ratios lower than 20.

High-frequency power conversion is useful for miniaturization of power electronics, but requires low loss passive components to achieve high power densities without thermal issues.

At COMPEL 2017, we presented a paper (link for pdf) investigating the lowest achievable ESR and the highest achievable power capability of a resonant tank using an air-core inductor with a single-layer foil winding and commercially available capacitors. A loss model is presented and online catalogs of multilayer ceramic capacitors are searched for components that can provide a low ESR when combined with an optimally designed inductor for various resonance frequencies.

The resulting resonator has a measured sub-mΩ ESR and high efficiency with 250 V dc rating in a 1 cm³ volume. The resonant tank, when used in a resonant switched-capacitor converter, has kilowatt-range power capability. A power converter, using this resonant tank, will be limited by the power density of switches and interconnects rather than by passive components.