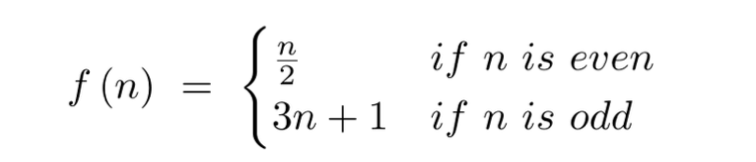This past September, mathematician Terence Tao of UCLA released a paper summarizing his near solution to a problem that has stifled the mathematical community for over three quarters of a century, “The Collatz Conjecture”. Given the function f(n) (shown below), plugging in an even value results in it being divided by 2, and plugging in an odd value results in it being multiplied by 3 and added to 1. The conjecture proposed by German mathematician Lothar Collatz in 1937 is that for any natural number n, the end result will always be 1. The example provided by Linkletter (2019) goes as follows:
“For example, let’s use 10. It’s even, so the rule says to divide by 2, taking us to 5. Now that’s odd, so we multiply 5 by 3 and then add 1, landing us on 16. Now 16 is even, so we cut it in half to get 8. Even again, so halving gets us 4. Now 4 is even, so we take half, getting 2, which is even, and cuts in half to 1.”
The issue facing mathematicians hoping to prove this conjecture is finding a way to show that it is true for all natural numbers n. So far, it has been proven for numbers with less than 19 digits, and supercomputers have the ability to check for numbers with hundreds or thousands of digits. However, this still does not prove the conjecture for all natural numbers.
Tao’s latest findings were published in a post titled Almost All Collatz Orbits Attain Almost Bounded Values. Collatz orbits are the sequences of numbers obtained when plugging a natural number into the function above. The Collatz Orbit for 10 is (10, 5, 16, 8, 4, 2, 1, 4, 2, 1, …). The orbit is “bounded” by 4, 2, and 1, because 2 is half of 4, 1 is half of 2, and 4 is 3 multiplied by 1 plus 1. So, the orbit will cycle through 4, 2, and 1 infinitely. What Tao demonstrates in his paper is that nearly all natural numbers have such orbits and thus satisfy the Collatz Conjecture. Although he was unable to prove the conjecture, his results suggest that the likelihood of a counterexample to the conjecture decreases logarithmically as you go further down the number line. In other words, Tao’s results suggest that the occurrence of potential counterexamples to the conjecture is rarer than previously proven.
A simple math riddle with a difficult solution has puzzled mathematicians for years, but Terence Tao has taken a huge stride towards discovering its solution. However, Tao believes that an entirely new approach than his may be needed to bring about the full solution to this problem. So, it may be some time before The Collatz Conjecture is put to rest.
An article by Joe Gyorda
View the original article:
https://www.popularmechanics.com/science/math/a29033918/math-riddle-collatz-conjecture/
View Tao’s Results:
https://terrytao.wordpress.com/2019/09/10/almost-all-collatz-orbits-attain-almost-bounded-values/