Here are the slides from my talk today at G2ELab in Grenoble.
Discussion of modeling winding and core loss, designs for kHz frequencies, designs and challenges for MHz frequencies, and new approaches to passive components for MHz frequencies. It includes a list of several dozen references at the end, and many of the slides include references numbers, so this can be a good entry point for finding more information on those topics.
At APEC 2017 we presented a resonant structure that improves the range and efficiency of wireless power transfer. High quality factor in resonant coils is essential for both goals, so developed a new technology that achieves Q values that weren’t previously possible. The new structure integrates inductive and capacitive effects to behave as an LC resonator. It’s made by stacking alternating layers of thin foil and dielectric material in a magnetic core. The high-Q is achieved through these effects:
We experimentally validated this structure and measured a Q of 1173 at 7 MHz despite a coil diameter of only 6.6 cm. Next, we integrated 2 of the structures into a wireless power transfer system. We were able to improve the range over which we could maintain efficiency above 94% by a factor of two when compared to the current state-of-the art. For more details see our presentation slides linked here, or our paper linked here.
At APEC 2017, we presented a high-Q resonator with a multi-layer winding and integrated capacitance for resonant power conversion.
A low-loss inductor winding for MHz frequencies can be built by connecting in parallel multiple layers of foil conductors much thinner than a skin depth. To ensure approxim
ately equal current sharing among layers, a capacitance can be inserted into each layer as shown in the figure; this is similar to twisting the litz wire for equal current sharing among wire strands. This capacitance can also be used for resonance, which eliminates the need for additional lumped capacitors and connection between capacitor and inductor.
We developed a method to implement this multi-layer winding by using copper laminated on polyimide substrates for ease of handling. The orientation of copper layers adjacent to the polyimide substrate ensures that there is no significant electric field, and hence low effective loss, in polyimide. The required capacitance for each layer is provided by free-standing PTFE films. The prototype of this resonator at around 8 MHz have a quality factor around 830 in under 15 cm3, 50% higher quality factor than an inductor with a single-layer thick foil winding connected to low-loss ceramic capacitors.
At APEC 2017, Benedict Foo presented a method for extracting winding resistance from an impedance measurement. For details on this method see the paper.
Impedance analyzer measurements can be helpful in assessing inductor a transformer winding resistance and predicting winding loss, but the measured ESR does not directly correspond to winding resistance. Neglecting the effects of core loss and winding capacitance can yield significant errors in the prediction. A step-by-step method to account for such effects and extract winding resistance from an impedance measurement is described. The proposed methodology is applicable to both inductors and multi-winding transformers. Several measurements are needed in this method; one is to determine the effects of core loss and the others yield the impedance from which winding resistance is extracted to form a resistance matrix. The winding resistance of a transformer was determined experimentally and the interactions between the winding resistance, effects of core loss, winding capacitance and inductance and their contributions to the measured impedance are demonstrated.
At the APEC 2017 magnetics industry session on Tuesday morning, I presented a talk that included:
The slides are available here.
I gave two presentations at the PSMA 2017 Magnetics Workshop. Brief summaries and slides are below.
Two-winding electrical core loss test setup.
The first was an introduction to core loss testing, and a survey of basic and advanced methods. Here are the slides: Survey of Core Loss Test Methods
It includes brief discussions of calorimetric methods and resonant methods. Calorimetric methods can be tedious, but are valuable as an independent check on other measurements. Resonant methods can improve accuracy at high-frequencies.
A simple 2:2 foil-winding transformer with current density and flux lines shown. In the top half, these are shown with the two windings excited with the same current, in phase. In the bottom half, they are 180 degrees out of phase. The losses are different by a factor of 4.
The second was a brief overview of magnetics modelling methods, including core and winding losses. The slides include a list of key references at the end.
As one example of what’s in the presentation, there’s an explanation of why it’s not adequate to model transformer winding loss with two frequency-dependent ac resistance values. As shown in this figure, the losses depend on the phase between the currents in the two windings, not just on their individual amplitudes. A model that correctly includes all the interactions between the windings is a resistance matrix.
Methods of finding the resistance matrix are discussed in the presentation and detailed in the references listed at the end.
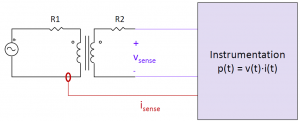
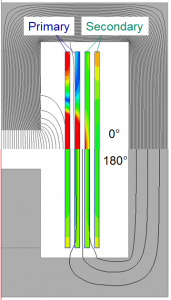
125-strand litz wire (5×25)
We’ve published a lot of papers on litz wire. Their emphasis has been academic, reporting new optimization results and calculation techniques. But they are are often too complex for design work, for an engineer who has many different issues to deal with. With that in mind, we took a different approach in a paper presented at APEC 2014, focusing on making the simplest possible design method that would still provide good practical guidance of litz wire design. We found a way to incorporate the results of some of our more sophisticated analysis into simple formulas that can be quickly and easily calculated in a spreadsheet or the like, so that you can get good recommendation for litz designs very easily.
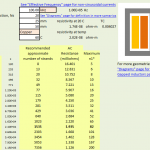
Spreadsheet main page
The full paper is available on our web site. The first two pages are all you need to read to get complete instructions on the method. To demonstrate how easy it is to use in a spreadsheet, here is the method implemented in a spreadsheet. You only need to put in four numbers–frequency, number of turns, core window breadth and turn length–and you get a range of options with the performance of each listed.
The simplest calculation is for a transformer winding, but the paper and the spreadsheet also include calculations for gapped inductors, accounting for the field in the region of the gap. Similarly the base method is for sinusoidal currents, but both include an easy adjustment to deal with nonsinusoidal waveforms.
There are some situations that this method can’t deal with–for example, if you have an unusual geometry, or multiple windings with different current waveforms in each winding. In those cases, our online LitzOpt calculator (which has recently been updated to be a little more robust and user friendly) can address most situations directly, or pretty much any situation in combination with an external field simulation.
In addition to being easier to use, the new method also features a calculation that helps you choose some of the details of the wire construction–how many strands are twisted together in each step. Typically one might combine somewhere between 7 and 50 strands in the first step, and then twist several of those bunches together in the second step, etc. The details of this sequence affect how well the wire eliminates skin effect. The later twisting steps should never combine more than 5 bundles together, but it’s often OK combine many 10s of strands in the first step. The new calculations tell you how many it’s OK to combine in that first step.
Another choice in the construction is the pitch of twisting at each step. This paper and spreadsheet don’t provide any guidance on that, but we are publishing a new paper on that topic at COMPEL 2014. That paper will appear here soon after the conference.
T
At COMPEL 2013, we presented an alternative self-resonant structure that can overcome various challenges associated with litz wire coils in the MHz frequency range. Link to full paper
The self-resonant structure is made of many layers of C-shaped thin foil conductors (much thinner than a skin depth) stacked in alternating orientation. A ballast capacitance is introduced by placing thin dielectric layers between adjacent conductor layers to force equal current sharing among the thin conductor layers.
This self-resonant structure has several advantages over conventional solid or litz wire coils connected to an ad
These advantages result in a calculated Q value of 1368 at 160 kHz for a structure with an 18 cm diameter.
A copy of the slides from this IEDMC plenary presentation is now available, with references for each topic added.
This presentation includes information on:
The information is from work in the field of inductor and transformer design for power electronics, and is targeted at a machine design audience, but is useful for high-frequency power transformer and inductor design as well.
Here is a pdf of the slides with references.
Nine different exhibits featured at the Tesla Tech Fair
The Tesla Tech Fair on April 4th was a great success. It featured panelists David Perreault and W. Bernard Carlson, author of Telsa, Inventor of the Electrical Age, which wasn’t available at the time of the event but is now available. It also featured nine different exhibits from Thayer and MIT students, staff and faculty.
The event got written up in The Dartmouth and The Valley News. There are collections of photos on Flickr from Thayer and from the Hop. The oneTesla team wrote a blog post about it as well.
Thanks to everyone who made this a success, including the Hopkins Center for the Arts and Thayer School of Engineering. The event was supported by the Office of the President and the Office of the Provost as part of Dartmouth’s Year of the Arts initiative.
